Surfing around yesterday I found the following link using a classpad calculator to assist students check their understanding of how to use the balancing method. It has worked fabulously well and yr10 students that typically hate algebra (and maths) are all smiles...
Here's the sequence of lessons up to this point (first week of term one)..
- review of algebraic terminology
- review of collecting like terms
- review of multiplying algebraic terms
- solving simple equations
I then introduced the balancing method saying we could get to the same result by making x the subject of the equation by examining the LHS and thinking what operation could we do to isolate the x value.
A student suggested that we subtract 5 and I said great.
Then I said to students that the crux of the balancing method was that anything we did on the LHS of the equation has to be done to the RHS. I wrote on the board
x + 5 = 7
x + 5 -5 = 7 - 5
x = 2
and asked how did that compare with our original answer. We then did the following example:
5x + 5 = 20
A student offered the following step:
5x + 5 - 5 = 20 -5
5x = 15
Typically students get stuck at this stage as 5÷5 =1 is not an intuitive step. For once I told them that I would divide by five and showed them how it works.
5x ÷ 5 = 15 ÷ 5 (please excuse the division symbol, I actually used fractions but it is too hard in html)
x = 3
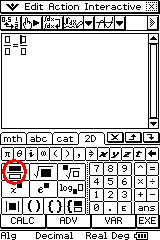
And here's the real magic.. I then took out CAS calculators borrowed from the senior school and they did a number of examples with them. For the following example:
2x - 2 = 15
Their brains started making connections and they actually were using the calculators to check that their logic was correct rather than to give them just answers.
 You can see from the example that each step in the calculator mimics the steps to answer the problem on paper. It is easy to see how after each operation (+2, ÷2) x becomes the subject of the equation and ultimately becomes solved with x=8.5
You can see from the example that each step in the calculator mimics the steps to answer the problem on paper. It is easy to see how after each operation (+2, ÷2) x becomes the subject of the equation and ultimately becomes solved with x=8.5Common errors become obvious earlier. Students decide what operation needs to be done and see what that operation would do. Take this common case:
 The student has multiplied by 2 before they have subtracted. They can instantly see their mistake (the LHS of the equation looks more complex rather than simpler so the student starts again. The second attempt subtracting 5 gets them closer to making x the subject of the equation.
The student has multiplied by 2 before they have subtracted. They can instantly see their mistake (the LHS of the equation looks more complex rather than simpler so the student starts again. The second attempt subtracting 5 gets them closer to making x the subject of the equation.For many of us, this is how we learnt to transpose equations - a little trial and error. Lots of practice. Lots of heartache. Lots of looking at the back of the book.
The students found using the calculator fun... and the calculator only gave them guidance - not just solving the answer. It was a mix between the old inverse operations method (change the sign/change the sign that causes all sorts of difficulties when fractional terms/multiple terms are introduced) and the balancing method. To be honest, I've never found the 'scales' explanation that typically accompanies the balancing method useful - but the CAS introduction way I think may have real promise.
The other great thing is that they were recording their answers really well on paper.
For the above example I would see (with equals signs aligned):
2x-2=15
2x-2+2=15+2
2x=17
2x÷2=17÷2
x=8.5
To see mid tier students lay out work like this rather than
1) 8.5
was fantastic.
Here is a link to other CAS calculator posts.