Trigonometric equations and the CAS calculator

There are lots of ways of solving trigonometric equations on the Classpad but I have avoided using Trisolve as it takes away the thinking aspect of trigonometric equations. Instead I focussed on setting up equations in eActivities with the intent to complement them with the Geometry section later.

eActivities are a great place to store frequently used equations. In this instance, I wanted to keep all of the trigonometric and circle equations in one place ie sine, cosine & tan ratios, sine rule, cosine rule, sector, segment equations, circumference, area.

To do this I opened an eActivity from the main menu.

Then I started a new eActivity by going File -> New. Then I saved it by going File->Save. I called it Trig Formulae.

So then I inserted a Numsolve strip to hold my equation.

Once the strip was added I used the soft keyboard to name it the Sine ratio. Then I pressed solve to put the equation in.

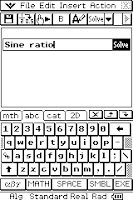
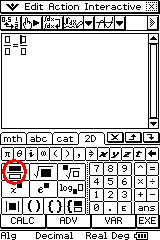
Using the mth tab in the soft keyboard and then selecting the Trig option at the base of the soft keyboard I entered 'sin('. Directly below the mth tab, the theta button can be found and then closed the bracket. Don't type the word 's' 'i' 'n' using the soft keyboard as it won't work - it will treat it as s x i x n.

Then using the 2D tab, I created a fraction and using the var option entered o ÷ h. I hit exe, then closed the equation using the x at the top left hand corner of the window.

I then tried it out using the example opp=7, hyp=14, theta = ? I left theta blank, made sure the angle was selected (with the dot next to it coloured in) and pressed solve in the toolbar. Viola, theta = 30°. If you get some weird answers check that the calculator is set in degrees mode. If the answer is still weird, reset the calculator and it seems to work.

Update (25/3/09): After using this with the class for a few days (especially with radians) I noticed a few strange results where the calculator would return unexpected answers (eg for the above example -330°). To fix this, set the Lower bound to 0 and the upper bound to 180 (for degrees) or pi/3.14159 (for radians) and the results will appear as expected.

I then set about putting in the cosine ratio.

It's a great tool for things like the cosine rule where students find it hard to transpose equations and forget negative signs or for circle, segment and sector equations that are commonly forgotten.

Here is a link to other CAS calculator posts.

Trigonometry and CAS calculator I

During exams last year we noticed that those who had CAS calculators were not using them for Trigonometry problems. During summer school we sought to rectify this. To start with we looked at properties of triangles.

Students stated that the calculator would give no solution when solutions existed. This sounded doubtful but I had a good idea where they were going wrong.

I started with the following. Take three lines, 4cm, 2cm, 1cm. Now obviously this can't make a triangle. Right?




No matter how we change the angles at A & B they cannot form a triangle. This was to inform students that a no solution result in their calculator had meaning.

So now we had a look at a problem that they were having difficulty with.

In their work pads they had written A=x, a=5cm, B=72°, b=72 and labelled the triangle correctly. So far so good.

They could tell it was a sine rule problem but had difficulty entering it into the calculator. Where did the sin, cos, tan buttons go from the calculator?

The first thing to do is find the sine function. Open the soft keyboard, select the mth tab and press the Trig button at the bottom of the keyboard.



Next enter the sine equation with the substituted values. They needed the fraction template inside the soft keyboard under 2D






Hitting execute at this point gives no solution. Huh?

Well.. we still have to solve for x. So highlight the equation and go to the interactive menu (in the menu bar at the top of the work pane), select Advanced and then solve. The Equation should be there and the variable listed should be x.



After a rather long wait a huge expression appeared with a strange looking answer.

I'll rekey it here as the whole answer does not appear on the work pane on the calculator.

{x=360.00.constn(1)+137.209, x=360.00.constn(2)+42.791}

The answers are the two bits in red (at this point we had a bit of a chat about the ambiguous case with the sine rule). To get to the answer you have to navigate with the style and the left/right arrows at the edges of the equation.



So the answer is x=137° or x=43° (0 d.p.)

We then drew these triangles to give students a better understanding of the ambiguous case.

In the next example we'll look at the perils of rounding and go back to the case above with the impossible triangle.


Here is a link to other CAS calculator posts.

3D trigonometry

3D Trigonometry in year 10 is one of those subjects that lots of kids have issues with. Students traditionally learn just one topic at a time, are tested and then move to the next topic. With 3D trigonometry are all of a sudden faced with using lots of maths all at once.

Topics that all come together:

• Parallel lines (in 3D)
• Alternate/Complementary/Supplementary etc angles
• Polygon properties
• Trigonometric ratios
• Pythagoras' theorem
• Sine Rule
• Cosine Rule
• Oblique and isometric drawing
• 3d visualisation
• Volume, Surface area
• Algebra (in all its guises)

My students have seen some success in this topic through the use of "wireframes" (made of skewers and connected with a hot glue gun) and templates placed in the wireframes to indicate various right angled and non right angled triangles. It also helps them see parallel lines and equivalent lengths/angles. This seems to be the concrete element they need to put all the other stuff in place.

I also try to introduce the topic multiple times throughout the year as new concepts are introduced (eg. parallel lines - > volume -> pythagoras -> trig ratios -> sine rule -> cosine rule)

Also useful is the discussion on solving triangles here.