Let's start with simple substitution into an equation:
a) Find y at x=3 for y = 2x^2 + 2x + 2
The "|" is important between the equation y = 2x^2 + 2x + 2 and x=3
Let's now find x if we know y. This is a little harder as we have to solve the equation.
b) Find x at y=14 for y = 2x^2 + 2x + 2
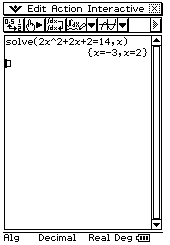
The easiest way to do this is to type 14 = 2x^2 + 2x + 2, highlight it using your stylus (this is important!) and then go
interactive->advanced->solve->ok
Note that it find both possible solutions (unlike using numsolve with the incorrect range specified)
Let's find the first derivative. For this use the 2D template in the soft keyboard
 Go keyboard -> 2D -> Calc ->
Go keyboard -> 2D -> Calc ->c) Find the 1st derivative of y=2x^2 + 2x + 2
Note that I removed the "y=" this time. I differentiated the expression on purpose as it makes the next part easier.
Finding the 1st derivative/gradient/instantaneous rate of change at a point is also easy.
d) Find the 1st derivative of y = 2x^2 + 2x + 2 at x = 3
As you can see, it is a mix between c) and a)
Last but not least we can find a point for a particular gradient.
e) Find x at y' = 14 for y = 2x^2 + 2x + 2

To find y itself we could repeat a)
It's very much a case of thinking what you need and then finding it. As you can see it can all be done with one line on a CAS calculator, things that would take multiple steps on paper. TanLine is also a useful function that can be investigated and used to quickly find tangents.
Viola!
Click here for more CAS calculator tutorials






